Continuity

Definition of continuous at a point #

A function $f$ is continuous at a number $a$ if $\displaystyle \lim_{x\to a} f(x) = f(a)$.

That definition tells us a lot! #

Writing $\displaystyle \lim_{x\to a} f(x) = f(a)$ means the following three things:

1. There is a point $( a, f(a) )$ on the graph; that is, $f(a)$ exists.
2. $\displaystyle \lim_{x\to a} f(x)$ exists
3. $\displaystyle \lim_{x\to a} f(x) = f(a)$ , that is, we can just plug in $a$ to find the limit!

Definition: Discontinuous at a point #

If $f$ is defined near $a$ but not defined at $x=a$, then we say that $f$ is discontinuous at $x=a$. Or, we say $f$ has a discontinuity at $x=a$.

Example #

Identify where the function is discontinuous:

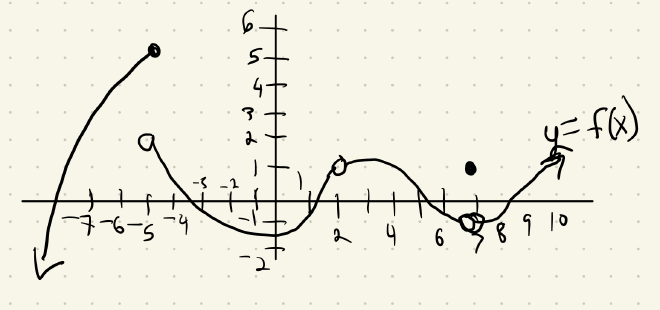
Solution:

Example #

Identify where the function is discontinuous:

1. $f(x) = \dfrac{3x^2 + 2x+1}{x-2}$

   Click to reveal the answer.

   Here the function is discontinuous at $x=2$. This is a jump type discontinuity (the graph jumps over the asymptote) It is continuous everywhere else.

2. $g(x) = \dfrac{1}{x^2}$

   Click to reveal the answer.

   Like above, the function is discontinuous at $x=0$. This is a jump type discontinuity (the graph jumps over the asymptote) It is continuous everywhere else.

3. $h(x) = \left\{\begin{align} \dfrac{x^2-4}{x-2} & \text{, if } x\ne 2 \\ 4 &\text{, if } x=2 \end{align} \right.$

   Hint: find a limit

   Click to reveal the answer.

   This one's neat! Since $\lim_{x\to 2} = 4$ (we did example in the [video in section 1.6](https://youtu.be/52EGYgkpNQs?t=244) and $f(2)=4$, the limit exists and equals the value of the function. It's continuous everywhere since we plugged the hole!

Continuity on an interval #

Note We define

• continuity from the left at a if $\displaystyle \lim_{x\to a^-} f(x) = f(a)$, and
• continuity from the right at a if $\displaystyle \lim_{x\to a^+} f(x) = f(a)$

Definition #

A function $f$ is said to be continuous on an interval $(a, b)$ if it continous for every number in the interval in $(a,b)$.

Example #

Revisiting our function from before, on what intervals is $f$ continuous?

Facts about continuity #

1. Polynomials are continuous everywhere - all $x$ values in $(\infty, \infty)$.
2. A rational function is continuous on its domain
3. Root functions, trig functions and exponentials and logarithms¹ are continuous on their domains.

If you still haven’t memorized the domains of trig functions, this would be a good time to take a moment to start. Especially the sine, cosine, and tangent functions.

Example #

Show that the piecewise function $$ f(x) = \left\{ \begin{align} x &\text{, if } x < 1 \\ \sqrt{x} &\text{, if } x \ge 1 \end{align} \right. $$ is continuous on $(\infty, \infty)$.

Example #

Please attempt the following example before checking the answer:

On what intervals are the following continuous?

1. $f(x) = x^3 -4x + 1$
2. $g(x) = \sqrt{x} + 2$
3. $b(x) = \dfrac{x^2 + 2}{x^2 + 4}$

Continuity and function algebra #

If $f$ and $g$ are continuous functions and the number $c$ is a constant, then the following combinations of functions are also continuous:

1. $f + g$
2. $f-g$
3. $fg$
4. $cf$
5. $f/g$ if $g(x) \ne 0$.

Additionally, if $f$ is continuous at $b$ and $\displaystyle \lim_{x\to a} g(x) = b$, then $$ \lim_{x\to a} f(g(x)) = f\left( \lim_{x\to a} g(x) \right) = f(b) $$

… that is, if $f$ is continuous there, we can pass the limit inside the function.

Example #

Evaluate $\displaystyle \lim_{x\to 2} \sin\left( \frac\pi4 x \right)$

Solution: Since $\displaystyle\lim_{x\to 2} \frac{\pi}{4}x = \frac\pi2$ and $\sin(x)$ is continuous at $x=\frac\pi2$, we can pass the limit inside the continuous sine function: $$ \lim_{x\to 2} \sin\left( \frac\pi4 x \right) = \sin\left( \lim_{x\to 2} \frac\pi4 x \right) = \sin\left( \frac\pi2 \right) = 1 $$

Example: #

Evaluate $\displaystyle \lim_{x\to 0} x^4 \cos\left( \frac1x \right)$

For this one, $\frac1x$ is discontinuous at $x=0$, so we cannot move the limit inside the cosine function! We need other tools to evaluate the limit. Give it a try (hint: Squeeze Theorem).

Intermediate Value Theorem #

Suppose that $f$ is continuous on a closed interval $[a, b]$ and let $N$ be any number between $f(a)$ and $f(b)$. Then there exists a number $c$ in $(a, b)$ such that $f(c) = N$.

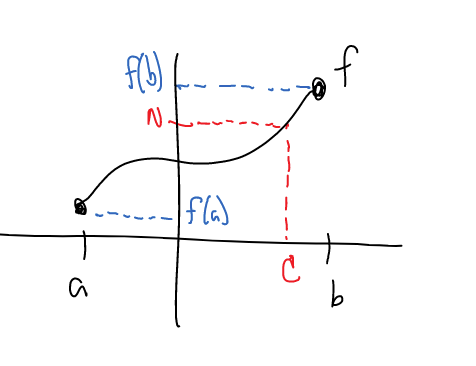
*somewhere between $a$ and $b$ there’s a number for which $f(c)$ hits the desired $y$-value of $N$.

Intuitively, if I’m Jabara Hall and want to walk to the Pod by the pond, I have to cross Perimeter² road. My travel is continuous - I can’t teleport or use a jet pack.

An application example #

Show that the function $f(x) = x^4 + x- 3$ has a zero in the interval (1,2)

Now practice! #

Head over to WebAssign and work on section 1.8. If you have questions, let me know!