Section 1.4

What is Calculus all about?

The Tangent Problem #

Tangent comes from the Latin word meaning “touching.” The idea is that given a particular curve and a point, we want to find a line which touching that curve at only that point. We call this the tangent line.

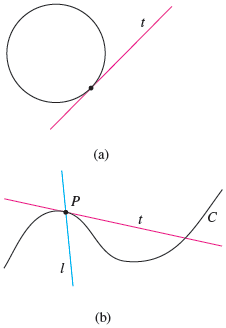
In this picture, part (a), the line $t$ is tangent to the circle. In part (b), the line $t$ is tangent to the curve at point $P$ near that point because near that point, it’s touching the curve at exactly one point. Looking outside the small interval around $P$, though, $t$ does pass through the curve in another place (making it a secant line), so thinking of “tangent” means thinking in a small neighborhood of a point!

Example #

Find an equation of the tangent line to the parabola $y=x^2$ at the point $P(1,1)$.

This example is from the textbook, and it looks at computing the slopes of secant lines (thought lines that pass through two points) near point $P(1,1)$. Here’s an excellent Geogebra exploration by WSU faculty Justin Mears which illustrates how the slopes get closer and closer to a particular value (what we’ll call a limit).

Please click this link and and explore the activity:

• You can grab point $Q$ and move it.
• Watch as the secant lines $PQ$ (red) get closer and closer to the tangent line (green), the slope $m_{PQ}$ gets closer and closer to a particular number.
• What is that number?

https://www.geogebra.org/m/c5479ucc

The Velocity Problem #

Here we’re asking the question - how fast am I going at this particular moment?

Remember that $\displaystyle \text{Velocity} = \frac{\text{Distance}}{\text{time}}$

Example #

Consider a ball thrown in the air, whose height $t$ seconds after it is thrown is given by $s(t) = 40t - 16t^2$ in feet. Compute the average velocity for the time periods beginning at $t = 2$ seconds and lasting 0.5, 0.1, and 0.05 seconds.

Can you estimate the instantaneous velocity when $t =2$?

The Area Problem #

We can compute the area of a rectangle really easily. Triangles are basically the same (just 1/2). Straight-edged shapes like stars, pentagons, etc? Easy! Just break them up into triangles and add them together.

It gets a little weirder when shapes are curved. How do we find the area of the bottom picture below?

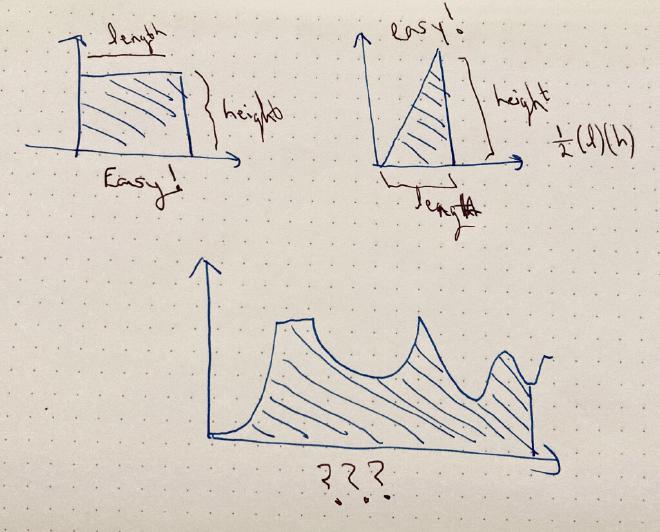
… the idea is that we’ll break it up into smaller shapes (rectangles / triangles) and add those up. But to be accurate, they need to be really, really small rectangles / triangles.

Integral Calculus was developed to answer this question! But it’s not just because we want to find areas.

The Distance Problem #

Distance = velocity * time.

In this situation, we know exactly how fast something is going. For example, our car is moving at some velocity $v(t)$. If the velocity is constant (for example, you have set cruise control to 75mph on the I-35), determining how far you go after a certain time is easy.

How far did you travel after 1 hour? 75 miles. After 2 hours? 150 hours. After 90 minutes? 112.5 miles.

What if your velocity varies (e.g. city traffic?). Sometimes you’re accelerating. Sometimes you’re cruising, sometimes you’re stopped at a stop light.

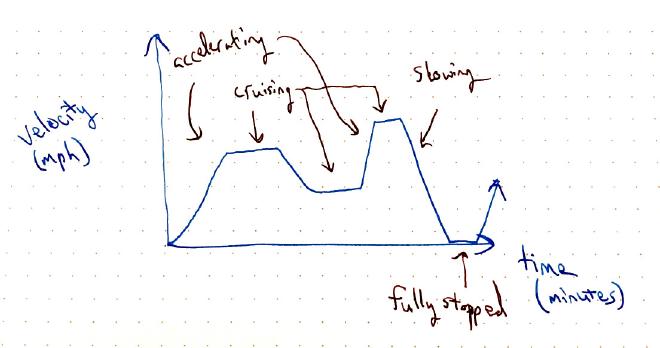
How can we determine how far you traveled? We can break up the time interval into smaller intervals and compute the velocity * time for each interval and then add them up. … this is actually the area problem!

Calculus is so cool!

Have a question? A comment? Want to clarify something above or on your homework set? Send me an email and let’s talk about it!