The derivative

The derivative as a function #

In the previous section, we found the derivative at a point which is a number.

We will consider the function $f’(x)$ given by: $$ f’(x) = \lim_{h\to 0} \frac{f(x+h) -f(x)}{h} $$ which gives the slope of the tangent line to the function $y=f(x)$ at any point $(x, f(x))$, whenever that limit exists.

Example: #

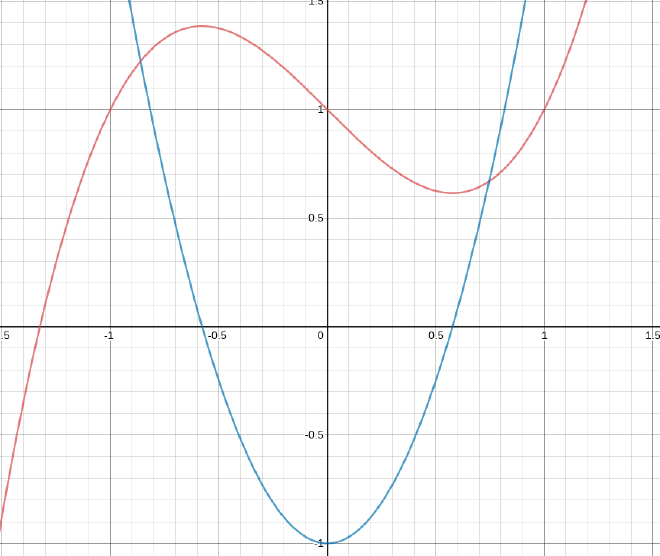
Let $f(x) = x^3 - x + 1$

1. Find the derivative $f’(x)$ of the function.
2. Graph both $f$ and $f’$ on the same coordinate axes.

Here’s the graph

Example #

Find the derivative of $f(x) = \sqrt{x-1}$ State the domain of $f’$.

Example #

Find the derivative of $\displaystyle f(x) = \frac{2+x}{1-x}$

Other Notations #

We’ll see many different notations both in this class and outside.

When a function is defined $y=f(x)$, we might write any of the following, which all mean the same thing:

• $f’(x)$
• $y’$ <— this notation we refer to as Newton’s notation¹.
• $\displaystyle \dfrac{dy}{dx}$ <— these are referred to as Leibniz notation²
• $\displaystyle \dfrac{df}{dx}$
• $\displaystyle \dfrac{d}{dx} f(x)$
• $\displaystyle D_x f(x)$ <— you’ll see this in Calc 3 and differential equations
• $\dot{y}$ <— this is actually Newton’s notation from Principia. Physicists often use this in homage to Newton.

If we want to evaluate the derivative of $y=f(x)$ at $x=a$, we can write:

• $f’(a)$
• $\displaystyle \frac{dy}{dx} \Large|_{x=a}$ <— a vertical bar saying “derivative at this number”
• $y’(a)$

As I said above, they all mean the same thing. If you’re ever unsure of notation, please ask!

Differentiability #

Definition #

A function $f$ is differentiable at $a$ if $f’(a)$ exists. It is differentiable on an open interval (a,b) [or $(a, \infty), (-\infty, b), \text{ or } (-\infty, \infty)$] if it is differentible at every number in the interval.

Example #

Polynomials, sine and cosine are nice and differentiable on $(\infty, \infty)$. Their derivatives, for reasons we’ll see later, are still polynomials, -cosine, and sine, respectively, whose domains are all real numbers.

Are there functions that aren’t differentiable?

Example #

Where is the function $f(x) = |x|$ differentiable?

When is a function not differentiable? #

• Discontinuities

• Cusps

• Vertical tangents.

VIDEO HERE

Higher Derivatives #

The second derivative is the derivative of the derivative of a function. For example, if $y=f(x)$, we’ll write:

• The first derivative if $f’(x)$ or $\dfrac{dy}{dx}$.
• The second derivative is $f’’(x)$ or $\dfrac{d^2y}{dx^2}$.

Example: #

Let $f(x) = x^3 - x + 1$, find $f’’(x)$

NOTE: we did $f’$ above

Even higher derivatives: #

Yes, we’ll go higher. We’ll see 3rd and 4th derivatives (and more in calc 2).

• $f’’’(x)$ is the third derivative <— last of the tick marks
• $f^{(4)}(x)$ is the fourth derivative
• $f^{(5)}(x)$ is the fifth derivative
• … and so on; the parentheses around the number mean derivative not exponent.

---

Physical interpretation of derivatives? #

Velocity is derivative of position with respect to time. …. Acceleration is derivative of velocity with respect to time.

Posting that video might make me seem like a jerk. But that’s $f’’’(x)$³.

Now practice! #

Head over to WebAssign and work on section 2.2. If you have questions, post them here, and either I or a fellow student will answer them quickly!