Derivatives of trig functions

Derivatives of Trig Functions #

We saw last time the derivatives of sine and cosine which will be repeated here:

• $\dfrac{d}{dx} (\sin (x)) = \cos (x)$

• $\dfrac{d}{dx} (\cos (x)) =- \sin (x)$

Let’s use them to derive¹ the rest of the formulas.

Tangent and cotangent #

• $\dfrac{d}{dx}( \tan(x)) = \sec^{2}(x)$

  We saw this last time, too. Use the quotient rule. If you don’t remember, try it again!

• $\dfrac{d}{dx} (\cot(x)) = -\csc^{2}(x)$

  Follow the same approach and use the quotient rule. Ask questions if you are unsure where to go.

Secant and cosecant #

• $\dfrac{d}{dx} (\sec(x)) = \sec (x) \tan (x)$

• $\dfrac{d}{dx} (\csc(x)) = \csc (x) \cot (x)$

  Repeat the above argument with cosecant and verify you can get this one.

Putting them all together #

Many examples #

1. Find the derivative of $y = x^2 \sec (x)$

2. Differentiate with respect to $t$, $y = \cos t + \sqrt{t}\sin(t)$

3. Find the slope of the line tangent to $y = 3x \sin x$ at the point $(\pi/2, 3\pi/2)$

Here’s a picture (the blue line is $y=3x$ while the green curve is $y=3x\sin x$).

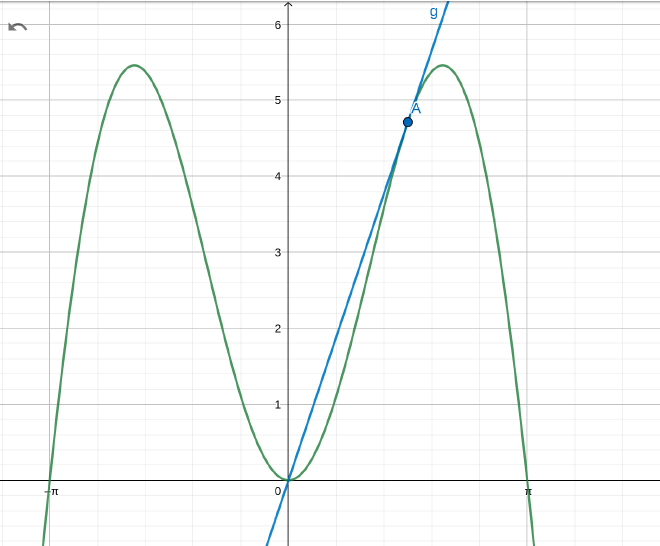
4. A ladder 20 ft long rests against a vertical wall. Let 𝜃 be the angle between the top of the ladder and the wall and let x be the distance from the bottom of the ladder to the wall. If the bottom of the ladder slides away from the wall, how fast does $x$ change with respect to $\theta$ when $\theta = \pi/4$?

VIDEO HERE

Now some limits #

Here’s an important limit that we’ll come back to often:

$$ \lim_{t \to 0} \frac{\sin t}{t} = 1 $$

and

$$ \lim_{t \to 0} \frac{\cos(t) - 1}{t} = 0 $$

Deriving the derivative of sine. #

Let’s use the definition of the derivative to find the derivative of $\sin x$.

$$ \frac{d}{dx} (\sin x) = \lim_{h \to 0} \dfrac{\sin(x + h) - \sin(x)}{h} $$

Finding more complicated limits #

Find the limit $\displaystyle \lim_{t \to 0} \dfrac{\sin(4t)}{\tan(20t)}$

Now practice! #

Head over to WebAssign and work on the exercises.

Have a question? A comment? Want to clarify something above or on your homework set? Let me know!