Implicit Differentiation

Implicit curves #

Some curves are defined implicitly as equations. They’re not necessarily functions, but we can still do calculus.¹

Example: #

The equation $x^2 + y^2 = 4$ defines a curve - a circle!

It consists of two implicit functions $y = \sqrt{4-x^2}$ and $y = - \sqrt{4-x^2}$, the upper and lower arcs of the circle, respectively.

Implicit differentiate #

• Our process is to take the derivative of both sides of the equation with respect to $x$.
• When you differentiate a $y$, we use the chain rule and multiply by $\frac{dy}{dx}$.

Example #

Differentiate $x^2 + y^2 = 4$ implicitly and solve for $\frac{dy}{dx}$, then find the points where $x^2 + y^2 = 4$ where the tangent line is horizontal and where the tangent line is vertical.

Example #

Find $\dfrac{dy}{dx}$ implicitly if $x\sin y + y\sin x = 1$

This is a really neat wobbly curve:

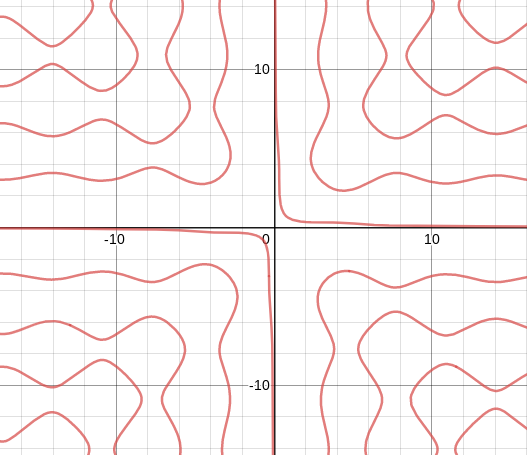
Here I’m using Geogebra to model the tangent line to the curve at any arbitrary point. Pretend that the curve models the shoreline; the tangent line would tell our GPS exactly how to hug the shore without crashing.

Check out this geogebra activity to play with it: (click this link)

https://www.geogebra.org/calculator/nzuk449p

---

The second derivative #

In order to find the second derivative with respect to $x$, we first need to solve for $\dfrac{dy}{dx}$ and differentiate that quantity.

The notation should help you remember this: $$ \dfrac{d^2y}{dx^2} = \dfrac{d}{dx}\frac{dy}{dx} $$

Example: #

Find $y’’$ of the curve $x^3 + y^3 = 1$

Example #

Find the equation of the of the tangent line at the point $(0, 1/2)$ of the curve $$ x^2 + y^2 = (2x^2 + 2y^2 - x)^2 $$

²