Section 4.1

Area, Distances, and Approximations

The Area Problem #

The motivation of this section is that we want to find the area that is under a curve, above the $x$ axis and between two endpoints. For example, consider the shaded region under the curve $f(x)=x^2$ on the interval $[0, 1]$:

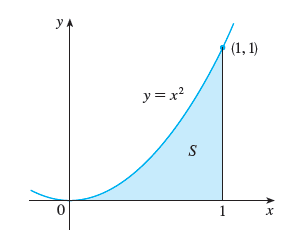
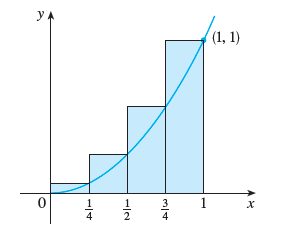
One approach is to approximate the area by cutting the region into rectangles. Let’s cut $[0, 1]$ into four pieces. The width of each rectangle then will be 1/4 and the height determined by the “right endpoint” as pictured here:

• The first rectangle’s right endpoint is at $x=1/4$, so its height is $f(1/4) = 1/16$

• The second rectangle’s right endpoint is $x = 1/2$, so its height it $f(1/2) = 1/4$

• The third rectangle’s right endpoint is $x = 3/4$, so its height it $f(3/4) = 9/16$

• The fourth rectangle’s right endpoint is $x = 1$, so its height it $f(1) = 1$

so we can over approximate the area to be = $\frac{1}{16} \cdot \frac14 + \frac14 \cdot \frac14 + \frac{9}{16}\cdot \frac14 + 1 \cdot14 = \frac{15}{32}$ or 0.46875. to get its decimal value¹.

… but that’s an over approximation. Let’s use left endpoints to under approximate to give us a range:

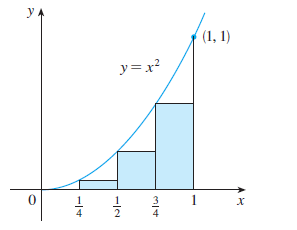
• The first rectangle’s right endpoint is $x = 0$, so its height it $f(0) = 0$ The area is $(1/4) \cdot 0$
• The second rectangle’s right endpoint is at $x=1/4$, so its height is $f(1/4) = 1/16$ The area is $(1/4) \cdot 1/16$
• The third rectangle’s right endpoint is $x = 1/2$, so its height it $f(1/2) = 1/4$ The area is $(1/4) \cdot 1/4$
• The fourth rectangle’s right endpoint is $x = 3/4$, so its height it $f(3/4) = 9/16$ The area is $(1/4) \cdot 9/16$

so we approximate the area by $0 \cdot \frac14 + \frac{1}{16} \cdot \frac14 + \frac14 \cdot \frac14 + \frac{9}{16}\cdot \frac14 = \frac{7}{32}$ or 0.21875.

So, we can say $$ 0.21875 \lt \text{ area under } x^2 \lt 0.46875 $$

That’s a pretty crappy approximation ², since we can obviously see massive over counting or undercounting in each graph.

A solution? More rectangles! Let’s try dividing the region into 8 rectangles:

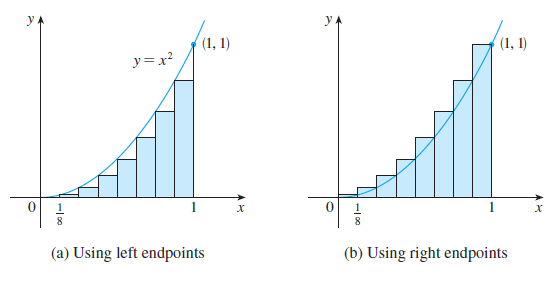
… and we can add even more! Here’s a video demoing going from 5 rectangles to 80 rectangles. Notice how the area values are getting closer and closer together. As though in the limit they will converge to the same number.

Here’s the geogebra activity if you’re curious.

Area as limit of a sum of rectangles #

If $f$ is a continuous function on the interval $[a, b]$, we divide the interval $[a, b]$ into a sequence of $n$ points: $x_1, x_2, x_3, \dots…, x_n$; these are the left or right endpoints of the rectangles. The height of each rectangle will be the value of the function, $f(x_i)$. The width of the rectangle will be $\frac{b-a}{n}$. Then the area under the function $f$ is defined to be $$ \text{Area} = \lim_{n\to \infty} f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + \dots + f(x_n) \Delta x $$

… it’s tedious to write blah + blah + blah + blah + blah … over and over, so mathematicians have a shorthand notation way of writing it, called “sigma notation.” We use $\Sigma$ because that is the Greek letter that makes the for “S” sound in “sum.”

We’ll write: $$ \text{Area} = \lim_{n\to \infty} \sum_{i=1}^\infty f(x_i) \Delta x $$

The $\Sigma$ notation for area is as follows:

$$ \begin{equation*} \sum_{\text{variable and starting point}}^{\text{upper bound}} \text{height * width} \end{equation*} $$

Evaluating areas #

Net Change: Distance, accumulation #

Remember how Distance = Velocity*Time? If we have a velocity function, we’ll use $v(t)$ to be the heights of rectangles, $\Delta t$ to be the widths, and estimate distance by using rectangles!

Example: #

The velocity graph of a braking car is shown. Use it to estimate the distance traveled by the car while the brakes are applied.

Example #

… so yeah, our textbook has the following exercise that definitely made me 😲. It’s about the original SARS outbreak in Singapore in 2003. ³

The shows the number of people per day who died from SARS in Singapore at two-week intervals beginning on March 1, 2003.

Date	Deaths per day
March 1	0.0079
March 15	0.0638
March 29	0.1944
April 12	0.4435
April 26	0.5620
May 10	0.4630
May 24	0.2897

Estimate the number of people who died of SARS in Singapore between March 1 and May 24, 2003, using both left and right endpoints.

After questioning my answers to myself, I learned that over the course of the roughly four months Singapore was affected, only 33 people died. China and Hong Kong were hit much worse in terms of lives lost.

Source: A. Gumel et al., “Modelling Strategies for Controlling SARS Outbreaks,” Proceedings of the Royal Society of London: Series B 271(2004): 2223–32. via Calculus by James Stewart

Endpoints and approximations #

If you’re given an interval $[a, b]$, then the left endpoints will start with $a$ and not use $b$; and the right endpoints will end on $b$ but not use $a$.

The height will always be the value of the function evaluated at the particular $x$ value.

For approximating the area, you’ll always add together the areas of the individual rectangles which is $f(\text{number}) \Delta x$:

$$ \text{Area} \approx f(x_0) \Delta x + f(x_2) \Delta x + f(x_2) \Delta x \dots + f(x_n) \Delta x $$

We can notice the common factor of $\Delta x$ and factor it out: $$ \text{Area} \approx \Delta x \left( f(x_0) + f(x_2) + f(x_2) \dots + f(x_n)\right) $$

Interpreting the meaning of more integrals #

Integration is usually framed as “area” under a curve, but as we saw above, it’s really always “adding together something times something else.”

Example #

$f(x)$ is the slope of the trail at a distance of $x$ miles from the start of the trail, what does $\int_3^5 f(x)\, dx$ represent?

Hint The ‘rectangles’ we’re multiplying are slope by distance.

Example #

A honeybee population starts with 100 bees and increases at a rate of $n’(t)$ bees per week. What does $100+\int_0^{15} n’(t)\, dt$ represent?

Hint: The ‘rectangles’ are rate of population increase per week multiplied by weeks.

Example #

If $w’(t)$ is the rate of growth of a child in pounds per year, what does $\int_5^{10} w’(t)\, dt$ represent?