section 6.3

Logarithms

Logarithmic functions #

If $b > 0$ and $b\ne 1$, the exponential function $f(x) = b^x$ has an inverse; we define that inverse function to be the logarithmic function with base $b$, denoted by $\log_b (x)$

$$ \log_b (x) = y \iff b^y = x $$

Examples #

Compute each of these values:

1. $\log_{3} 81$
2. $\log_5 125$
3. $\log_5 \frac{1}{25}$
4. $\log_4 2$

Cancellation equations #

• $\log_b (b^x) = x$ for every real number $x$, and

• $b^{\log_b(x)} = x$ for every $x>0$.

Logarithmic facts / properties of logarithms #

In all of these properties, we’ll assume $b > 1$ ¹

• The logarithmic function $f(x) = \log_b(x)$ has a domain $(0, \infty)$;

• $x=0$ is a vertical asymptote of the function

  That is, $\displaystyle \lim_{x\to 0^+} \log_b(x) = -\infty$

• $\log_b 1 = 0$ for every base $b$.

• $y = \log_b (x)$ is an increasing function.

  That is, $\displaystyle \lim_{x \to \infty} \log_b(x) = \infty$

• $\log_b(xy) = \log_b(x) + \log_b(y)$

• $\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)$

• $\log_b(x^c) = c \log_b(x)$ ²

… most of these properties we’ve seen in our various courses before this one, but it’s important to note about them they are just rules of exponents!

• “How do you multiply same base, you add exponents” … $\log_b(xy) = \log_b(x) + \log_b(y)$
• “How do you divide same base? You subtract exponents” … $\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)$
• “How do you raise a power to a power? Multiply the exponents!” … $\log_b(x^c) = c \log_b(x)$

The Natural Logarithm #

For the natural base $e$, we define the natural logarithm to be $$ \ln x = \log_e(x) $$ We donate it by “ln” because it’s from the French logarithme naturel

Everything we said above can be repeated just with the base $e$.

Note: $\ln x = y \iff e^y = x$

Yeah, but why are we talking about logarithms now? #

“I already knew that stuff about logarithms from precalculus/algebra. Why is it the last thing we’re talking about in calculus!?!” you might be saying.

The natural logarithm gives the area under the hyperbola $\frac1x$. That is, we can define the natural logarithm by the equation

$$ \ln(x) = \int_1^x \frac1t \, dt $$

so that $\ln(a) = \int_1^a \frac1x \,dx$:

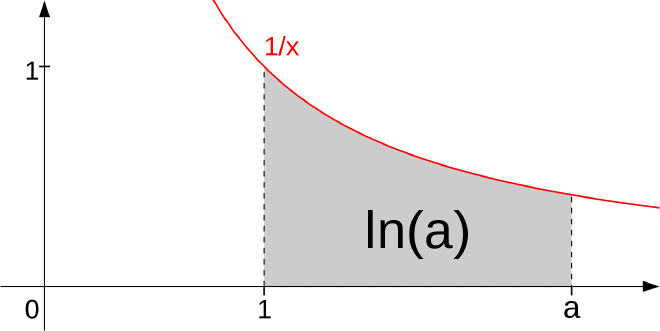
It turns out that this exact integral satisfies all of the properties of a logarithm! AND it is also the inverse of the exponential function. I find that exciting, but it’s not directly related to this course. Maybe a teaser of things to come…³.

Now try some homework! #

You have the tools you need to cover the basics of the homework. This section is really just review in disguise, so you probably will have questions but it’ll mostly come back to you. Ask me questions if you have them!