Section 3.1

Critical Numbers, Max and Mins

Critical Numbers #

Definition A critical number of a function $f$ is a number $c$ in the domain of $f$ such that $f’(c) = 0$ or $f’(c)$ does not exist.

Example #

Find all critical numbers of the function $f(x) = x^{3/5}(4-x)$.

Why are these critical? #

When $f’(c) = 0$, that means that the function $f$ has a horizontal tangent line at the point $x=c$. That is, it’s either a peak or a valley of the graph of $f$.

When $f’(c)$ is undefined, that means that the function $f$ has a vertical tangent line at the point $x=c$. As we’ll see in coming sections, this means the function is changing shape at that point as well.

Example #

Find critical numbers of the function $f(x) = x^{1/3}$.

Solution Since $f’(x) = \frac{1}{3} x^{-2/3} = \frac{1}{2x^{2/3}}$ (use the power rule), we can see that $x=0$ makes the derivative undefined. That means $x=0$ is a critical number.

Now let’s look at the shape of the graph $y=x^{1/3}$. Notice that the function has a vertical tangent line at $x=0$ and how the function goes from being curved up like a cup ◡ on the interval $(-\infty, 0)$ to being curved down like a frown ◠ from $(0,\infty)$:

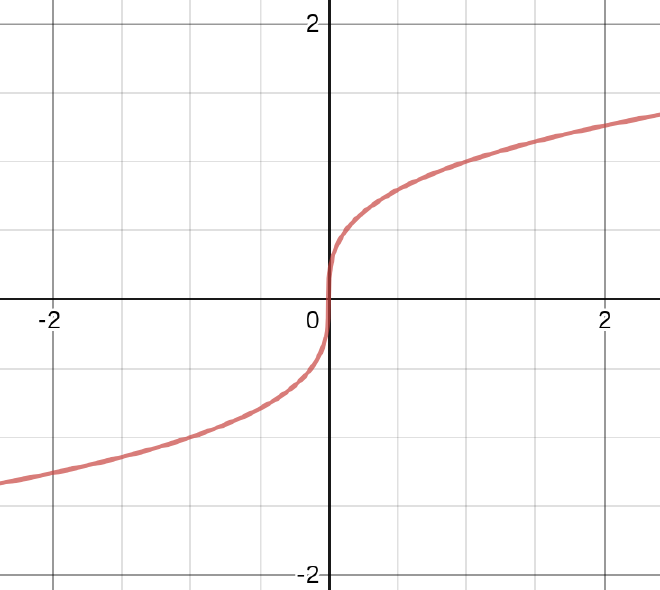
… this has everything to do with the critical number, as we’ll see when we discuss concavity in a future section!

Maximum and Minimum Values (Extrema) #

Note that the plural of maximum is maxima, the plural of minimum is minima, and when we want to talk about multiple extreme (max/min, not 🤘) values, we’ll call them extrema.

Absolute Max / Absolute Min #

The number $f(c)$ is a:

• absolute maximum value of $f$ if $f(c) \ge f(x)$ for all $x$ in the domain.

  This is the highest possible point of the graph.

• absolute minimum value of $f$ if $f(c) \le f(x)$ for all $x$ in the domain.

  This is a lowest possible point of the graph.

Note that there may be only one absolute maximum / absolute minimum. It’s also possible that a function not have an absolute max/min.

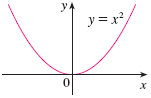
For example, $y=x^2$ has an absolute minimum value of 0 at $x=0$, but it has no absolute maximum.

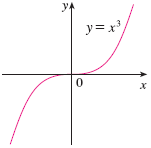
On the other hand, $y=x^3$ has no minimum or maximum values.

Local Max / Local Min #

The number $f(c)$ is a:

• local maximum value of $f$ if $f(c) \ge f(x)$ when $x$ is near $c$.

  This is a “peak” of the graph.

• local minimum value of $f$ if $f(c) \le f(x)$ when $x$ is near $c$.

  This is a “valley” of the graph.

There can be more than one local extreme value.

Some examples #

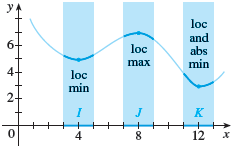
Here’s an example graph showing a function which has multiple local minimum values: one at $x=4$ with output value 5, one at $x=12$ with output value 3. It has one local maximum at $x=8$ with output value $x=6$. It has no absolute maximum, but it does have an absolute minimum at $x=12$ with minimum value $3$.

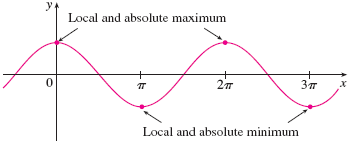
Here’s another graph demonstrating the $\cos x$ has local maxima for every multiple of $2\pi$: $0, \pm 2\pi, \pm 4\pi, \dots$ and local minima for every odd multiple of $\pi$: $\pm \pi, \pm 3\pi, \pm 5\pi, \dots$. Because these are also the highest and lowest points the graph ever attains, they are also absolute extrema.

The Extreme Value Theorem #

If $f$ is continuous on a closed interval $[a, b]$, then $f$ attains an absolute maximum value $f(c)$ and an absolute minimum value $f(d)$ at some numbers $c$ and $d$ in the interval $[a, b]$.

Simply put, on a closed interval, we’re guaranteed that a continuous function will attain an absolute maximum and minimum value. Because it can’t blow up to infinity, it must reach a high and a low point.

Fermat’s Theorem #

If $f$ has a local maximum or local minimum at $x=c$, then $c$ is a critical number of $f$.

Examples: #

Here are two very common examples:

1. $f(x) = x^2$ has a minimum value at $x=0$ the bottom of the U. Since $f’(x) = 2x$ is zero when $x=0$, we see that $x=0$ is in fact a critical number of $f$.

2. $g(x) = |x|$ has a minimum value at $x=0$, the bottom of the V. Since $f’(x)$ doesn’t exist at $x=0$, we see that $x=0$ is a critical number of $f$.

“The Closed Interval Method” #

Our textbook refers to this as the “closed interval method.” We’re simply using the Extreme Value Theorem. To locate an absolute maximum or minimum of a function, we:

1. Look for critical points of a function
2. Find the value of the function at the critical numbers.
3. Find the value of the function at the endpoints of the interval.
4. Pick the biggest for the maximum and the smallest for the minimum.

A just-math example #

1. Find the absolute extrema of the function on the given interval: $g\left( t \right) = 2{t^3} + 3{t^2} - 12t + 4\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ { - 4,2} \right]$

2. Find the absolute extrema of the function on the given interval: $g\left( t \right) = 2{t^3} + 3{t^2} - 12t + 4\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ { 0,2} \right]$

A physics example #

Between $0^\circ$ C and $30^\circ$ C, the volume $V$ (in cubic centimeters) of 1kg of water at a temperature $T$ is given approximately by the formula $$ V = 999.87 - 0.06426T + 0.0085043T^2 - 0.000679T^3 $$ Find the temperature at which water has its maximum density.

Note This says at temperature $T=0$, which is freezing, the volume of 1kg of water is approximately 999.87 cubic centimeters or basically 1 liter. That’s so cool and makes you wish we used the metric system like everyone else¹ 🙄

Note 2: This is a very slowly changing function on that interval. You can see the graph on Desmos by clicking this link: https://www.desmos.com/calculator/5uummrxtns

Okay, let’s solve the problem! I’m going to say “Using WolframAlpha” many times below. Click that link to take you to the actual calculation and see the results.

1. Start by finding the derivative: $V’(T) = -0.0002037 T^2 + 0.0170086 T - 0.06426$.

2. Find critical numbers: $V’(T)$ is a polynomial, so it’s always defined. And using WolframAlpha, we find that $V’(T)$ occurs when: $$ T\approx 3.96651 \text{ and } T \approx 79.5318 $$ Since only $T \approx 3.96651$ is in the interval $[0, 30]$, this is the only one we’ll consider.

3. Now, use the critical number and endpoints to find the volume of the water. $V(0) = 999.87$ cubic centimeters. $V(30) \approx 1003.76$ cubic centimeters ( again using WolframAlpha), and finally $V(3.96651) \approx 999.745$ cubic centimeters (if you’re not using WolframAlpha yet for these calculations, please do).

4. Finally, we need to interpret our answer. We were asked to find the temperature at which water has its maximum density. Density is inversely proportional to volume: $\text{Density} = \dfrac{\text{mass}}{\text{volume}}$ So we the maximum density will occur at the minimum volume.

💥 Water has the minimum density when the temperature is approximately $3.96651^\circ$ C. 🤯