Section 3.2

The Mean Value Theorem

In this section we’re going to explore the concept of a location where a function attains the average or or mean value.

It’s not mean 😡 , but mean 🧮.

We’ll start with Rolle’s theorem that tells us if something went up and came back down, there had to be a time when its derivative is 0.

Rolle’s Theorem #

Let $f$ be a function. If the following properties are true:

1. $f$ is continuous on the interval $[a, b]$
2. $f$ is differentiable on the interval $(a, b)$, and
3. $f(a) = f(b)$

then there is a number $c$ in the interval $(a,b)$ so that $f’(c) = 0$.

Some pictures: #

Here are some (ugly, hand-drawn) graphs showing examples

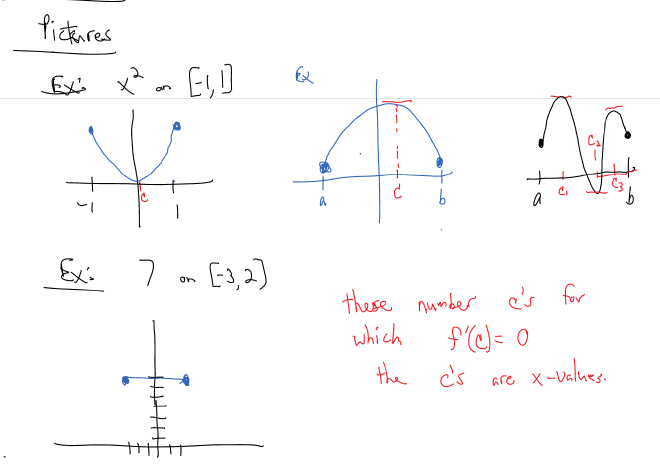
Example #

Verify the hypotheses of Rolle’s Theorem and find all values $c$ from the conclusion for the function on the given interval: $$ f(x) = 5-12x + 3x^2 \text{ on } [1, 3] $$

The Mean Value Theorem #

The basic idea is if you have a differentiable function on an interval, there is some point whose tangent line has the same slope (is parallel) as the secant line between endpoints. Here’s a picture from wikipedia:

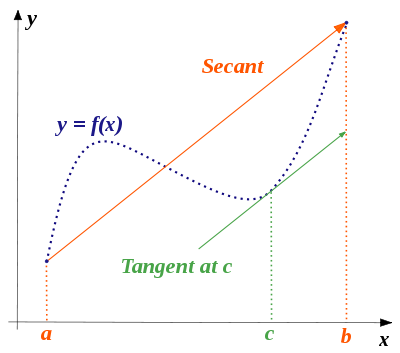
Formal statement of the Mean Value Theorem #

Let $f$ be a function. If the following properties are true:

1. $f$ is continuous on the interval $[a, b]$
2. $f$ is differentiable on the interval $(a, b)$, and

then there is a number $c$ in the interval $(a,b)$ so that ¹ $$ f’(c) = \dfrac{f(b)-f(a)}{b - a} $$

or, equivalently, $$ f(b) - f(a) = f’(c)(b-a) $$

By the way, if this looks like the slope formula or the point-slope form of a line, good! It’s all related!

Note: The Mean Value Theorem tells us that there is a number $c$ in the interval, but it doesn’t tell us what it is. For that, we will need algebra.

Example #

Determine all numbers $c$ that satisfy the conclusions of the Mean Value Theorem for the following function $$ f\left( x \right) = {x^3} + 2{x^2} - x\hspace{0.25in}{\rm{on}}\hspace{0.25in}\left[ { - 1,2} \right] $$

Example #

Suppose that we know that $f(x)$ is continuous and differentiable on the interval $[3, 10]$, and let’s also suppose that we know that $f(3) = -2$ and the $f’(x) \le 8$. What is the largest possible value of $f(10)$?

An Example #

You enter the I35 turnpike at 4:15pm at mile marker 57 (the 21st street entrance) You take exit 127 for Emporia at 5:00pm. No highway patrol officers caught you speeding. But was there a time when you should have been pulled over?

{{ < spoiler > }}

The Mean Value Theorem says that if $f$ is a continuous function on the closed interval and differentiable on the open interval $(a, b)$, then there is some $c$ in $(a, b)$ such that $$ f’(c) = \dfrac{f(b)-f(a)}{b - a} $$ Interpreting $f(t)$ to be the distance in miles traveled down the turnpike after $t$ time hours, then we can plug in $t = 0$ for 4:15pm and $t=3/4$ for 5:00pm (since we can think of going from from 0 hours to 3/4 of an hour for our journey). Then $f(0) = 0$ (we haven’t traveled yet), and $f(3/4) = 127 - 57 = 70$

The MVT tells us there is some value $c$ between 0 and 3/4 hour such such: $$ f’(c) = \dfrac{f(3/4) - f(0)}{3/4 - 0} = \dfrac{70 - 0}{3/4 - 0} \approx 93.33 \text{mph} $$

So although your didn’t get caught (maybe, say, Waze told you about a speed trap), your average speed was over 90mph, and there was some time between 4:15 and 5:00 when you were doing it, you little lawbreaker, you! 😈

{{ </ spoiler > }}

A real world example(?) #

Here’s a photo of a bridge in Beijing celebrating the MVT

²

Two more related results #

Theorem If $f’(x) = 0$ for all $x$ on an interval $(a,b)$, then $f$ is constant on $(a, b)$

Theorem If $f’(x) = g’(x)$ for all $x$ in the interval $(a,b)$, then $f - g$ is constant on $(a, b)$. That is $$ f(x) = g(x) +c \text{ where } c \text{ is some constant.} $$

Example #

Let $f(x) = x^2$ and $g(x) = x^2 + 42$. Notice that

$f’(x) = 2x$ and $g’(x) = 2x$ for any $x$ on all $(-\infty, \infty)$. Then we know the functions $f$ and $g$ must differ by a constant; that constant is $42$.

I’m going to, in my own colloquial way, call these functions “cousins”. They share the same derivative, so they’re in the same family of functions³. This is an important thing we’ll discuss more when we get to integral calculus!