↓Skip to main content
  1. Math 242: Calculus 1/
  2. Chapter 3/

Section 3.3

Table of Contents

The First and Second Derivative Test

Increasing / Decreasing Test #

  • If $f’(x) > 0$ on an interval, then $f$ is increasing on that interval.
  • If $f’(x) < 0$ on an interval, then $f$ is decreasing on that interval.
  • If $f’(x) = 0$ on an interval, then $f$ is constant on that interval.

Example #

Find where $f$ is increasing and decreasing. $$ f(x) = \frac34 x^4 + 2x^3 - 12x^2 + 5 $$

The First Derivative Test #

Suppose that $c$ is a critical number of a continuous function $f$.

  1. If $f’$ changes from positive to negative at $x=c$, then the function $f$ has a local maximum at $x=c$
  2. If $f’$ changes from negative to positive at $x=c$, then the function $f$ has a local minimum at $x=c$.
  3. If $f’$ doesn’t change sign at $x=c$, then $f$ has no local max/min at $x=c$.

Example #

Find the local maxima and minima of $f(x) = x + 2\sin x$ on the interval $[0, 2\pi]$.

Concavity #

We’ll define concavity on an interval in connection to a function’s shape related to its tangent lines on that interval. But the basic intuitive idea is that a function is:

  • Concave up if it’s shaped up like a cup ◡

    If you poured your favorite beverage into the function, it would hold it. 🍺 😄

  • Concave down if it’s shaped down like a frown ◠

    If you poured your favorite beverage into the function, it would spill 💧 😢

Concavity and tangent lines #

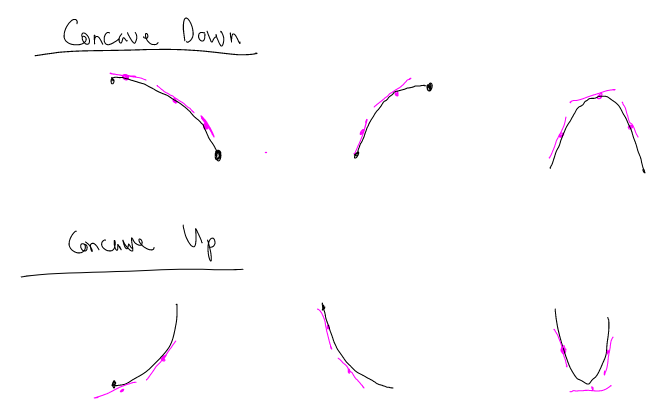
We define a function to be concave up on an interval if the function is always above its tangent lines on that interval.

We define a function to be concave down on an interval if the function is always below its tangent lines on that interval.

Concavity test #

  1. If $f’’(x) > 0$ for all $x$ in an interval, then $f$ is concave upward on that interval.
  2. If $f’’(x) < 0$ for all $x$ on an interval, then $f$ is concave down on that interval.

A point is called an inflection point if a function is continuous at the point and changes concavity from up to down or down to up at the point.

Example #

Find the inflection points and determine the concavity of the function $$ f(x) = x^4 - 2x^2 + 3 $$

The Second Derivative Test #

Suppose that $f’’$ is continuous near $x=c$:

  1. If $f’(c) = 0$ and $f’’(c) > 0$, then $f$ has a local minimum at $x=c$
  2. If $f’(c) = 0$ and $f’’(c) < 0$, then $f$ has a local maximum at $x=c$.

Note that this uses the second derivative to tell us about extrema. The value $x=c$ is a critical number, but it $f’(c)$ must be defined and 0 at that point.

Example #

Find local extrema of the function $$ f(x) = x^4 - 2x^2 + 3 $$

Example #

Using concavity, inflection points, and local extrema, sketch a graph of the function $$ f(x) = x^4 - 4x^3 $$

↑