Section 3.4

Section 3.4, Infinite Limites

Motivation: #

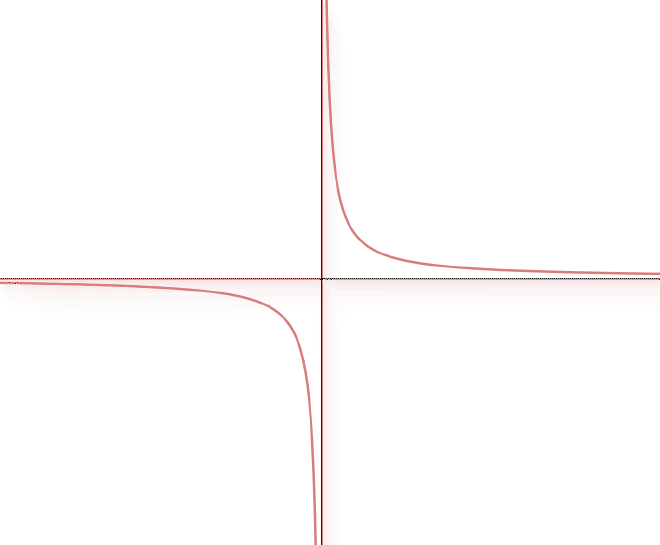
We’ve already seen $\displaystyle \lim_{x\to \infty} \frac1x = 0$. Also, since those $x$ values are positive, we’re approaching 0 from above.

On a similar note, $\displaystyle \lim_{x\to -\infty} \frac1x = 0$ as well. And since those $x$ values are negative, we’re approaching 0 from below. This matches what we know the graph to look like:

Intuitive Definition of the Infinite Limit #

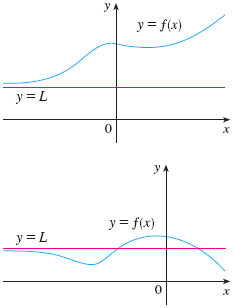
Let $f$ be a function defined on some interval $(a, \infty)$. Then $$ \lim_{x\to \infty} f(x) = L $$ means that the values of $f(x)$ can be make arbitrarily close to $L$ by requiring $x$ to be sufficiently large.

Examples of infinite limits where $f(x) \to L$ as $x\to \infty$.

Analogously, if the function is defined on $(-\infty, a)$, then we can have $\displaystyle \lim_{x\to -\infty} f(x) =L$ if $f(x)$ gets arbitrarily close to $L$ as $x$ get sufficiently large in the negative direction.

Horizontal Asymptote #

We call the line $y=L$ a horizontal asymptote of the function if $$ \lim_{x\to \infty} f(x) = L $$ or $$ \lim_{x\to -\infty} f(x) = L $$

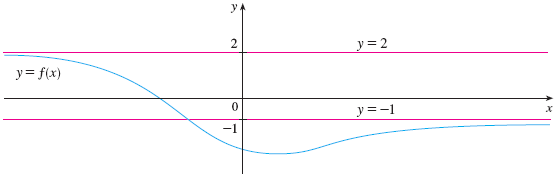
More than one horizontal asymptote? #

Yes! We call $y=L$ a horizontal asymptote. It’s entirely possible a function has more than one! Here’s an example curve with two horizontal asymptotes:

Computing Limits at Infinity #

First, we get a tool we’ll use to compute these infinite limits.

Theorem #

If $r \gt 0$ is a rational number, then $$ \lim_{x\to \infty} \frac{1}{x^r} = 0 $$ and if $r\gt 0$ is a rational number so that $x^r$ is defined for all $x$¹, then $$ \lim_{x\to -\infty} \frac{1}{x^r} = 0 $$

Example #

Now let’s compute an infinite limit. Evaluate

$$ \lim_{x \to \infty} \frac{2x^2 - 3x - 5}{3x^2 + 4x + 1} $$

Example #

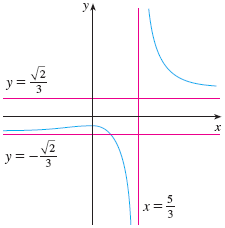
Find the horizontal and vertical asymptotes of the graph of the function.

$$ \frac{\sqrt{2x^2 +1}}{3x - 5} $$

Here’s an image that shows the asymptotes:

Example #

This example is a little different. Is “$\infty - \infty$” equal to 0? Or something else?

Compute $\displaystyle \lim_{x\to \infty} \sqrt{x^2 + 1} - x$

Example #

Here’s a very similar looking example

Compute $\displaystyle \lim_{x\to \infty} \sqrt{x^2 + x} - x$

… so “$\infty - \infty$” can be 1/2? Yes! In fact it could be any number or even $\infty$.

Infinite Limits at infinity #

When functions continue to grow in the positive (or negative) direction without bound, we write

$\displaystyle \lim_{x\to \infty} f(x) = \infty$ or $\displaystyle \lim_{x\to \infty} f(x) = -\infty$

But notes that $\infty$ is not a number, so our limit laws do not apply!

As we saw above, “$\infty - \infty$” could be anything, so we have to be careful such as in the following example:

Example #

Evaluate $$ \lim_{x \to \infty} 2x^2 - 3x $$ Solution Don’t plug in $\infty$! Otherwise this might happen:

Instead, factor first! $$ \begin{align*} \lim_{x \to \infty} 2x^2 - 3x &= \lim_{x\to \infty} x(2x - 3) \end{align*} $$ but since both $x$ and $2x-3$ grow to $\infty$ as $x$ grows large, we can say $$ \lim_{x \to \infty} 2x^2 - 3x = \infty $$

Example #

Evaluate $$ \lim_{x\to \infty} \dfrac{3x^2 - 4x + 5}{x+5} $$