section 5.1

Areas

We have found areas under the curve which are the signed area between a function and the $x$ axis, but what about finding the area between two different functions?

Example #

Find the area between $y = x+1$ and $y=-x+3$ between $x=1$ and $x=2$.

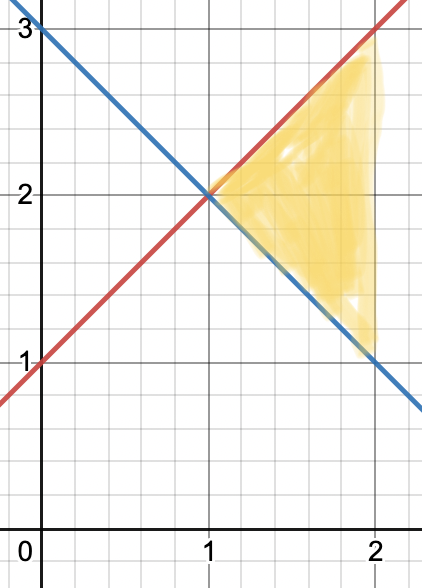
We’ll do this two ways.

1. Method 1: a. Find the area under the red curve: $\int_1^2 x+1 \,dx$ b. Find the area under the blue curve: $\int_1^2 -x + 3 \,dx$ c. Subtract those two areas in order to remove the region of overlap and leave us with the yellow shaded area pictured above. $$ \left(\int_1^2 x+1 \,dx \right) - \left( \int_1^2 -x + 3 \, dx \right) $$
2. Method two: Use properties of integrals to compute a single integral: $$ \int_1^2 (x+1) - (-x + 3) \, dx $$

Method two gives rise to the following generalization:

Finding the area between two curves #

If $f(x)$ and $g(x)$ are continuous functions on an interval $[a, b]$ and $f(x) \ge g(x)$, then the area between the two functions is given by: $$ \text{Area} = \int_a^b f(x) - g(x) \, dx $$

It is always

$$ \text{Area} = \int_a^b \text{upper function} - \text{lower function} \, dx $$

Example #

Find the area above $y=x^2$ and below $y=x$ between $x=0$ and $x=1$.

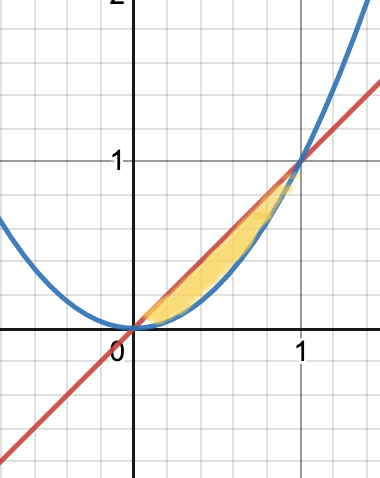
Solution by thinking about $x$ variables:

Solution version two, integrating with respect to $y$:

Example #

Find the area of the region bounded by the curves $y=\sin x, y=\cos x, x=0$, and $x=\pi/2$.

For this region, notice how the upper/lower function change roles:

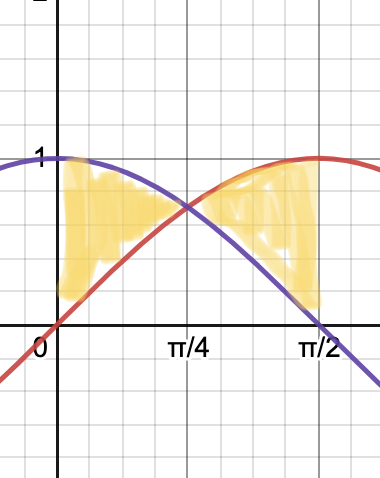
On the interval $[0, \pi/4]$ cosine is the larger function, while on the interval $[\pi/4, \pi/2]$ it is the sine function that is the upper function. For this reason, we need to split the area integral at $x=\pi/4$:

$\begin{align*} \text{Area} &= \int_0^{\pi/4} \cos x - \sin x \,dx + \int_{\pi/4}^{\pi/2} \sin x - \cos x \, dx \ &= \left(\sin x - (-\cos x) \right) \Big|{x=0}^{\pi/4} + \left((-\cos x) - \sin x \right) \Big|{x=\pi/4}^{\pi/2} \ &= \left[ \left(\sin(\pi/4) + \cos(\pi/4) \right) - \left( \sin(0) + \cos(0) \right)\right] + \left[\left(-\cos(\pi/2) - \sin(\pi/2) \right) - \left(-\cos(\pi/4) - \sin(\pi/4)\right)\right] \ &= \left[\frac{\sqrt{2}}{2} + \frac{\sqrt2}{2} - 0 - 1 \right] + \left[0 - 1 + \frac{\sqrt2}{2} + \frac{\sqrt{2}}{2} \right] \ &= 2\sqrt{2} - 2 \end{align*}$

Example #

Find the area between the curves $y=x^2 + 1$ and $y=-x+3$

Example #

Find the area of the region bounded by $x=2y^2$ and $x+y = 1$