section 5.2

Volumes by Washers

This section explores the ideas of computing volumes of solids by a method called ‘washers.’

---

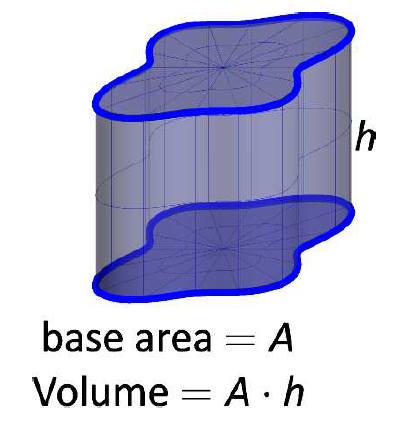
In general, the volume of a right cylinder is always (Area of the Base)*(Height).

For example, the volume of our common circular cylinders (e.g. toilet paper tubes) can be found by $V = \pi r^2 h$, that is, area of the base $\pi r^2$ multiplied by height $h$.

But cylinders need not be just circles. Here’s an example with a swirly base, but the volume will always be area of the base multiplied by height.

¹

---

Solids of revolution #

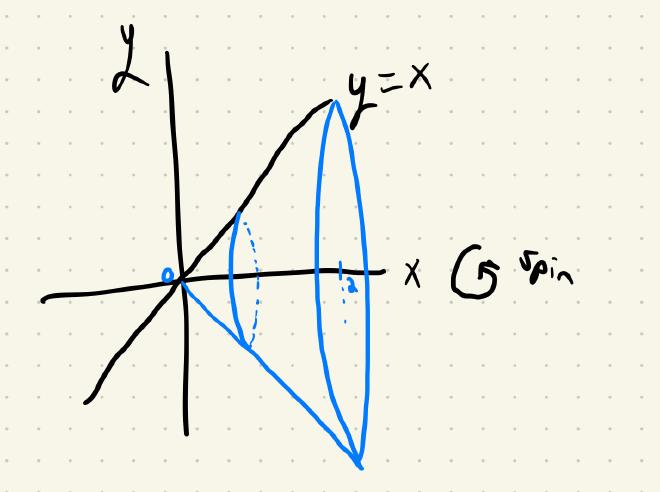
Imagine we have a function but we want to spin it over the $x$ -axis. If it’s a the line $y=x$ between 0 and 2, we end up getting a cone:

If we rotated it over the $y$-axis, it’d still be a cone, but oriented in a different direction:

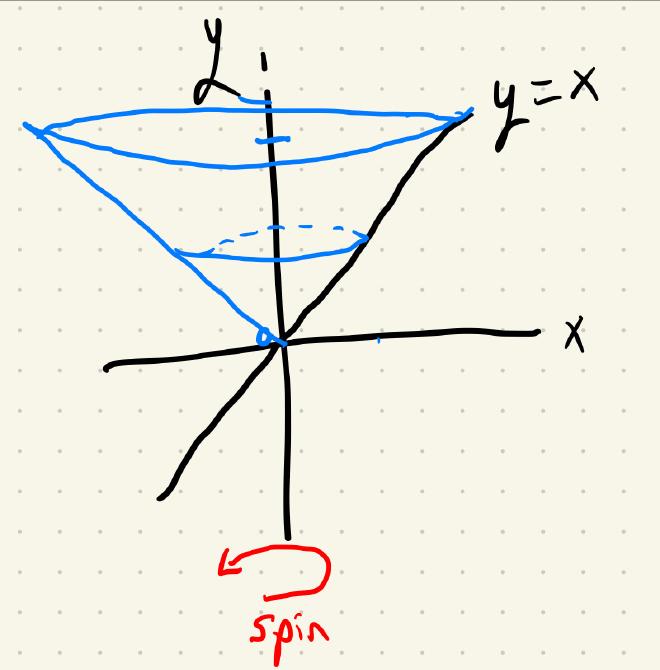
These are solids of revolution. They are solids that are generated by revolving a curve over an axis.

Volumes of Solids of Revolution #

Our strategy for this section is to find the volume of each solid by adding together infinitesimally small cylinders. To get started, let’s explore the example of the cone generated by revolving $y=x$ over the $x$ axis between $x=0$ and $x=2$:

Formula for the volume of a solid of revolution #

Let a solid be formed by revolving the curve $𝑦=𝑓(𝑥)$ from $𝑥=𝑎$ to $𝑥=𝑏$ around a horizontal axis, and let $𝑅(𝑥)$ be the radius of the cross-sectional disk at $𝑥$. The volume of the solid is given by

$$ V = \int_a^b \pi (R(x))^2\ dx $$

Notice the pieces: the volume of the tiny cylinder (area of the base * height) is given by, $\pi (R(x))^2$, which is the area of the cross-sectional disk, multiplied by $dx$, which is the height.

Example #

Find the volume of the solid obtained by revolving the region bounded by $y=x^2$, $x=0$ $x=2$, and $y=0$ over the $x$-axis.

Example #

Find the volume of the solid obtained by revolving the region bounded by $y=x^2$, $x=0$ $y=4$, and $y=0$ over the $x$-axis.

Volume by washers #

A washer is just a disk with a hole in it:

²

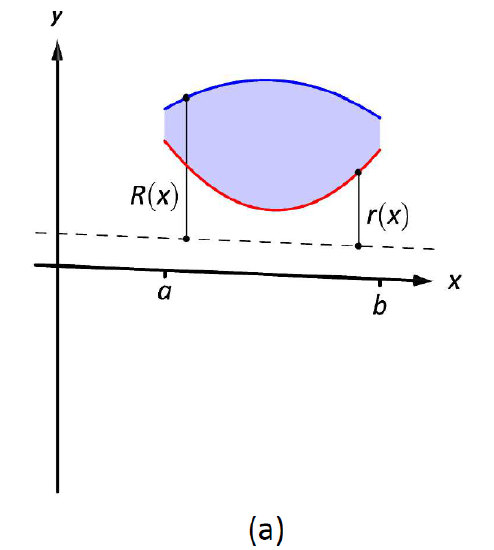
In this situation, we’ll be finding volumes of solids that have a void in the center, such as a cup, vase, or tube might have. For example, consider this region bounded between two functions on the interval $[a, b]$, revolved over the $x$ axis. It generates the following shape:

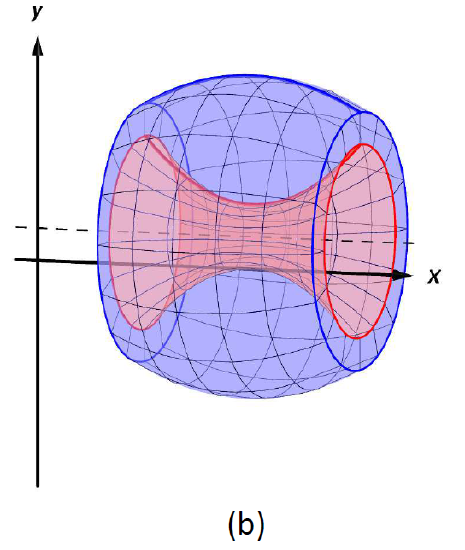
Volumes by Washers idea #

Just as we found the area between two curves by finding the difference between the upper and lower integrals, we’ll find the volume we want by finding the volume of the solid on the outside and subtracting the volume of the solid on the inside.

Our strategy is the following, if $R(x)$ is the upper radius and $r(x)$ is the inner radius: $$ \begin{align*} \text{total volume} &= \text{outer volume} - \text{ inner volume} \ &= \int_a^b \pi (R(x))^2 \, dx - \int_a^b \pi (r(x))^2 \, dx \end{align*} $$

Putting it all together, we have the following formula, if $R(x)$ is the outer radius and $r(x)$ is the inner radius of the region bounded between $[a, b]$:

$$ \text{volume} = \int_a^b \pi \left( (R(x))^2 - (r(x))^2 \right) \, dx $$

Example #

Find the volume of the solid formed by rotating the region bounded by $𝑦=𝑥^2$ and $x=y^2$ about the $𝑥$-axis.

Example #

We don’t need to revolve only about an $x$ or $y$ axis, we could do any line!

Find the volume of the obtained by revolving the region bounded by $y=x$, $x=1$, $y=0$ about the line $y=-1$.

Example #

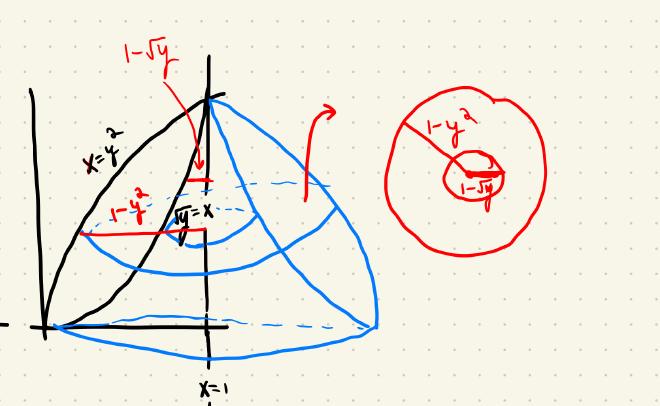
Find the volume of the solid obtained by rotating the region bounded by $y=x^2$ and $x=y^2$ about the line $x=-1$

Example #

Set up an integral to find the volume of the solid obtained by rotating the region bounded by $y=x^2$ and $x=y^2$ about the line $x=1$

Summary on axes #

For the washer method, if we are rotating a region over the $x$ axis, or any other line $y=c$ where $c$ is any number, then we will be integrating with respect to the $x$ variables. (Remember the $x$ axis is $y=0$)

If we’re rotating over the $y$ axis or any line $x=k$ where $k$ is any number, then we integrate with respect to the $y$ variables.

… and one more thing, distances are “bigger thing minus smaller thing,” so if the axis of rotation is to the right of the function, it’ll be (axis) - (function); if the axis is to the left, it’ll be (function) - (axis).

$V = \int_a^b \pi(R(x) - \text{axis})^2\, dx$ if we’re revolving over the line $y=\text{axis}$.

… it just happens to be that if it’s the $x$ axis, $\text{axis} = 0$, so $(R(x)-0)^2 = (R(x))^2$, so it all comes out in the wash(er).