section 5.3

Volumes by Cylinders

In this section, we’re still revolving regions over an axis, but rather than constructing our region as accumulating circles, this time we’re accumulating cylinders.

Open this Geogebra activity and slide the “Slide Me!” slider back and forth to see how the curve is revolved about an axis and how the “cylindrical shell” inside is being generated.

https://www.geogebra.org/m/SWBXZQxR

The surface area of a cylinder. #

Just as we did previously, we’ll compute volume as area*dx, but this time the areas that we’re accumulating are surface areas of cylinders. So how do we find that?

Imagine cutting a cylinder (such as a toilet paper tube) and unrolling it. The area will be circumference of the base multiplied by height:

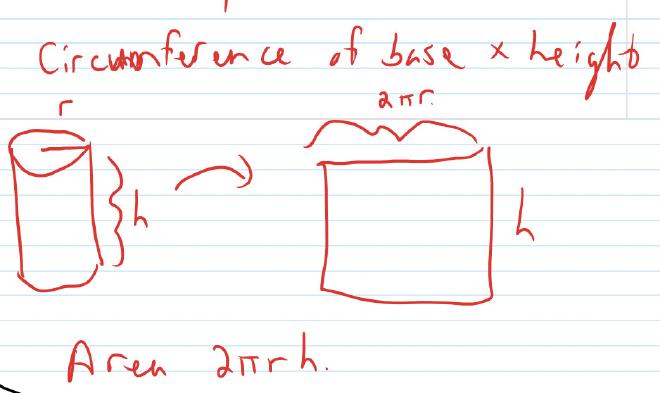
So the area will be $2\pi r h$ where $r$ is the radius and $h$ is the height.

Example #

Find the volume of the solid obtained by revolving the region bounded by $y=\sqrt{x}, y=0, x=1$ about the $y$-axis.

Example #

Find the volume of the solid obtained by revolving the region bounded by $y=3, y=8, x=0,$ and $x=4$ about the $x$ axis.

Example #

Find the volume of the solid obtained by revolving the region bounded by $y=x^2$, $y=0, x=1, x=2$ about the line $x=4$.

Comparing the disk/washer method #

Washer method Rotating a region bounded by $x=a$ to $x=b$,

1. Sketch the region being rotated and sketch the rotation
2. Sketch a typical disk/washer
3. Find the inner and outer radii
4. If rotating over a vertical line, integrate with respect to $y$; If rotating over a horizontal line, integrate with respect to $x$.
5. Area function is $A(x) = \pi (\text{outer radius})^2 - \pi(\text{inner radius})^2$ (using $x$ or $y$ depending on what we’ll integrate with respect to.
6. Volume is $\int_a^b A(x)\,dx$ or (or $y$’s).

Cylindrical Shell Method

1. Same Sketch the region being rotated and sketch the rotation
2. Sketch a typical cylinder
3. Find the radius and height of the cylinder
4. If rotating over a vertical line, integrate with respect to $x$ If rotating over a horizontal line, integrate with respect to $y$
5. The area function is $A(x) = 2\pi (\text{radius})(\text{height})$
   using whatever variable we integrate with respect to.
6. Same. Volume is $\int_a^b A(x)\,dx$ or (or $y$’s).

Example #

(If possible) Setup the integral to find the volume of the region bounded by $y=x^3$, $y=8$, $x=0$ about the line $x=2$ using both the washer and disk methods.

Example #

(If possible) Setup the integral to find the volume of the region bounded by $y=\sin(x)$, $y=0$, $x=\pi$ about the $y$ axis using both the washer and disk methods.