section 5.4

Work

Applying integral calculus to practical problems

¹

First, a couple refreshers from Physics #

Units #

“Units are your friend,” – Dr. Elizabeth Behrman

Measurement	SI Units	‘American’
Mass	kg	…
Distance	m	ft
Velocity	m/s	ft/s
Acceleration	$\text{m/s}^2$	$\text{ft/s}^2$
Force	N=$\text{kg m/s}^2$	lb
Work	J = N m = $\text{kg m}^2/\text{s}^2$	ft-lb
Density	$\text{kg/m}^3$	$\text{lb/ft}^3$

Formulas #

• Recall that Force = mass * accelation $F=ma$

• Work is force exerted for a distance $W = Fd$

Example, worked two ways #

If I push a 2kg book with constant acceleration $1 \text{m/s}^2$ over the table 5m, how much total work is acted on the book?

Solution 1: #

First, find the force: $\begin{align*} F &= ma \ &= ( 2\text{kg} ) ( 1 \text{m/s}^2 ) = 2 \text{N} \end{align*}$

Second, find the work: $\begin{align*} W &= Fd \ &= ( 2\text{N} )( 5 \text{m} ) \ &= 10 \text{Nm} \ &= 10 \text{J} \end{align*}$

Solution 2: #

Let’s graph with force along the $y$ axis and distance along the $x$ axis.

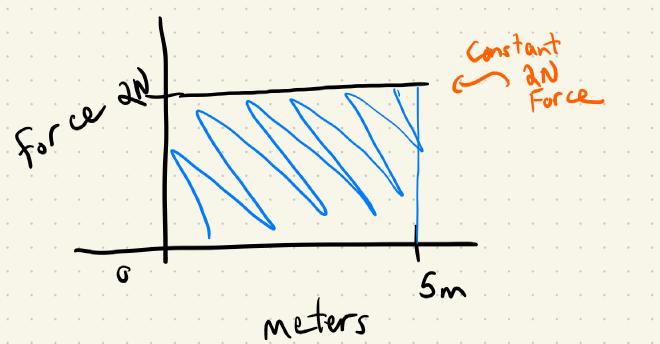
Since our time ranges from $x=0m$ and $x=5m$, we could compute the integral with the function $f(x) = 2\text{N}$

$\begin{align*} W = \int_{0\text{m}}^{5\text{m}} 2 \text{N} \, dx &= (2\text{N}) x \Big|_{x=0m}^{5m} \ &= (2\text{N})(5 \text{m})- (2\text{N})(0\text{m}) \ &= 10 \text{N} \end{align*}$

Force varying across distance #

What if the force changes at different points through the distance? In this example, let’s imagine that from 1 meter to 2, we are exerting more and more force. From 2 meters to 3, we push at a consistent force of 3 N; after three meters, we’re tired so we back off our force down; from 4 to 5 meters, it’s a consant 5 meters.

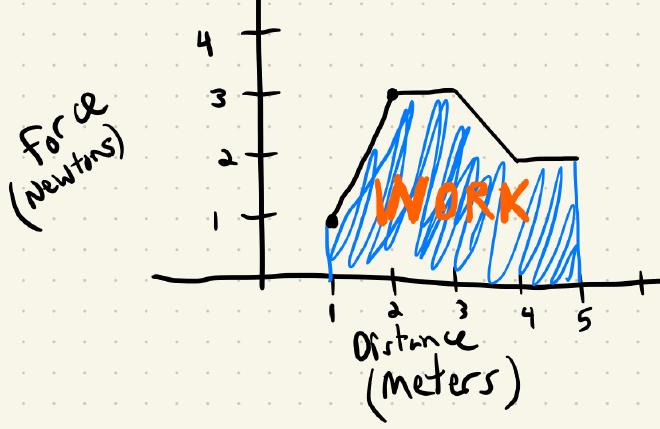
Let’s find the work using integrals!

$\begin{align*} W &= \int_1^5 f(x) \, dx \ &= \int_1^2 f(x) \, dx + \int_2^3 f(x) \, dx \ &= \int_3^4 f(x)\, dx \ &= \int_4^5 f(x) \, dx \ &= 2 + 3 + 1.5 + 1 \ &= 7.5 \text{Nm} \ &= 7.5 \text{J} \end{align*}$

Example #

A particle moves along the $x$ axis at a force of $\dfrac{10}{(1+x)^2}$ pounds at $x$ feet from the origin. Find the work done moving the particle to 9 feet from the origin.

Solution: Here the force is $f(x) = \dfrac{10}{(1+x)^2} \text{lb}$. So $\begin{align*} W = \int_a^b f(x) \, dx &= \int_{0}^{9\text{ft}} \dfrac{10}{(1+x)^2} \text{lb} \, dx \end{align*}$ … integrate (hint: $u$-substitution $u=1+x$) … and so the force is $9 \text{ft-lb}$.

Hooke’s Law #

The force exerted on a spring is directly proportional to the distance past its natural length

$F = kx$ wehre $x$ is the distance from the natural length and $k$ is the spring constant

Example #

Suppose $2\text{J}$ of work is required to stretch the spring from its natural length of 30cm to 40cm. How much work is needed to stretch from 35cm to 45cm?

Work to empty a tank #

Here’s the process we’re going to follow (I’m typing this out for future reference, jump down to the example):

1. Define a coordinate system Figure out where your origin should be
2. Find the cross-sectional area of a “sheet” of water Just as we found cross-sections of washers / cylinders when computing volumes
3. Find the volume of that “infinitesimal sheet” of water Since Volume = Area * height: Volume = Area $dx$
4. Find the force that is exerted on the sheet Force = volume*density
5. Find the work needed to “lift” the sheet out Work = Force * distance This will define a function which varies on distance.
6. Find the total amount of work required. … the sum of all infinitesimal work will be an integral!

Example #

Imagine a rectangular pool with dimensions 15ft x 8ft x 4ft is filled with 3ft of water. Find the amount of work that is needed to pump all of the water from the pool over its side [use the fact that water’s density is $62.5 \text{lb/ft}^2$].

Example #

An example with a variable cross-sectional area. Ex: Find the work required to empty the water from a full, hemispherical pool which has a diameter of 10ft, pumping the water directly over the edge.